Spoofing Realistic Credit Card Data for your Test Systems using Data Masker
Grant Fritchey shows how to use Data Masker to create fake credit card data that not only looks like the real thing, but also has the right distribution, so will act like it too, when we query it.
Data protection and privacy regulations, ranging from GDPR to HIPPAA to PCI, among many others, put strict compliance requirements on the storage and use of personal and sensitive data, in any of your systems. There is no distinction between development, test or production databases, in the event of a data breach. If such data is lost or compromised while it’s being used in any part of your DevOps processes, then the organization can face hefty fines and even criminal prosecution.
Balanced against this overriding need for compliance, is the need of the development team to be able to work with data that looks and acts “real”. How do you get around this conundrum? In this article, I’ll review how we might use a tool like Data Masker not only to obfuscate data, but also to ensure that the masked data reflects the characteristics and distribution of the real thing. I’ll use credit card data as an example, but similar principles apply to other types of data.
The challenges of faking data realistically
If the database we need for our development and testing contains sensitive or personal data, be it names, phones numbers or credit card numbers, then the answer might seem obvious: simply replace all this data with randomly-generated names or numbers. The immediate problem with this is that the resulting data will neither look nor act ‘real’.
To make the data look real requires a bit of thought and effort; let’s take credit card data as an example. To mask this data realistically, your data replacement ruleset must, firstly, use the standard format of credit card numbers, i.e. four sets of four numbers, such as 1234 5678 9012 3456, although you’ll also see 15 digits for American Express. It will also need to ensure that each replacement number is unique (more than one person can share a credit card, but for billing purposes, it’s one card).
So, our replacement method could invoke a random number generator, or a set of them, one for each of the four sets of numbers, which guaranteed a unique set of random numbers in the correct format. Job done? Not quite because, of course, the numbers in a credit card are not random.
In the United States, and based on my research this seems to be accepted around the world, the credit card numbers are assigned by the American National Standards Institute (ANSI), the same organization that defines the SQL language, among other things. They maintain the Issuer Identification Number database. The first six digits of your credit card define the institution that issued your card. So, if you have a Venture MasterCard issued by CapitalOne, I know that the first six numbers of your card are 552851. Further, the first one or several numbers will quickly identify the type of card. In the case of a MasterCard, the first two numbers will always be 51 or 55. A Visa card will start with 4. You can also see if the card was issued by an airline, an oil company or a telecommunications company, based on that first digit.
The next 9 (or up to 12) digits are your personal identifier within the issuing organization, your GUID or IDENTITY value, if you will. The last digit is a checksum value, used with a Luhn algorithm. All this is defined at the infographic on this Quora answer. On Simple-talk.com, Phil Factor shows how to apply the Luhn test in T-SQL, to verify the basic validity of a credit card number.
Is any of this important? It is if you want your ‘faked’ data not only to look real, but also act real. Your data will have a distribution; your credit card data will contain a specific, probably higher, proportion of Visa and Mastercard customers versus other cards. Depending on the type of data you’re dealing with, your location, and the business, your set of credit card data may contain ‘skew’. For example, if you’re in the travel and entertainment industry then you may have more credit cards than average that start with the number 3 (American Express). If you also have a lot of the same IIN values (that three-number identifier in the back of your card), you could have serious skew on your data.
This distribution is reflected in the statistics and histograms used by your SQL Server database system to determine the appropriate data retrieval strategy (a.k.a. execution plan), depending on the number of rows it expects to be returned by the query. If your data replacement method leaves you, instead, with a ‘random’ distribution then, of course, the performance and behavior of your queries against this data, in the test systems, won’t reflect what you’ll see in production.
If we want realistic looking data in a specific distribution, then we’ve just added another level of complexity to our processes, so what do we do?
Faking data realistically using Data Masker
Fortunately, Redgate’s SQL Data Masker tool has some credit card intelligence built into it. It can make credit cards that resemble Visa, Mastercard, American Express, Diners and Discover, and it will allow you to generate a specific data distribution.
Let’s see how that could work. In this article, I’m using a very simple database with a single table and a simple set of (mainly) 16-digit numbers, generated using RAND(). The script to create all of that is located CreditCardSetup. If I run Listing 1 against my initial test data set, it will reveal the distribution of the data.
|
1 2 3 4 5 6 7 |
SELECT CAST(COUNT(*) * 100.0 / (SELECT COUNT(*) FROM dbo.Creditcard AS c2) AS NUMERIC(4, 2)) AS CreditTypePct, LEFT(c.CreditCard, 1) AS CreditCardType FROM dbo.Creditcard AS c GROUP BY LEFT(c.CreditCard, 1) ORDER BY CreditCardType; |
Listing 1
The results look like this, and as you can see, we have a very even distribution across nine card types, which is not realistic.
| CreditTypePct | CreditCardType |
| 9.60 | 1 |
| 11.30 | 2 |
| 11.30 | 3 |
| 10.10 | 4 |
| 11.80 | 5 |
| 12.50 | 6 |
| 12.70 | 7 |
| 10.80 | 8 |
| 9.90 | 9 |
Let’s now see how we can use Data Masker to replace these random numbers with valid credit card numbers, reflecting each of the major card suppliers, and in a sensible, realistic distribution.
If you had access to the real data, or just to the statistics and histograms for that data, so you knew the real data distribution, then you could mimic that using the tool. You’ll see how to do this in another article. Here, however, I’ll just mimic a relatively normal credit card data distribution, for the USA at least. The Nilson Report provides this global distribution of transactions to arrive at the following distribution:
- Visa: 50%
- MasterCard: 25.6%
- UnionPay: 19.8%
- American Express: 2.5%
- JCB: 1.1%
- Diners/Discover: 0.8%
Setting up the data masking ruleset
I’m not going to outline all the details of setting up a Masking Set and Masking Rules; for complete documentation of SQL Data Masker, go here. However, I’ll explain enough that you’ll understand how to use multiple rules to arrive at data that both looks and acts real
Figure 1 shows the set of rules that I’m using to simulate the distribution of credit card information above. I’ve omitted the JCB data, and simulated the UnionPay data (using the Diners and Discover card type) because at this time, these two credit card types aren’t supported by SQL Data Masker.
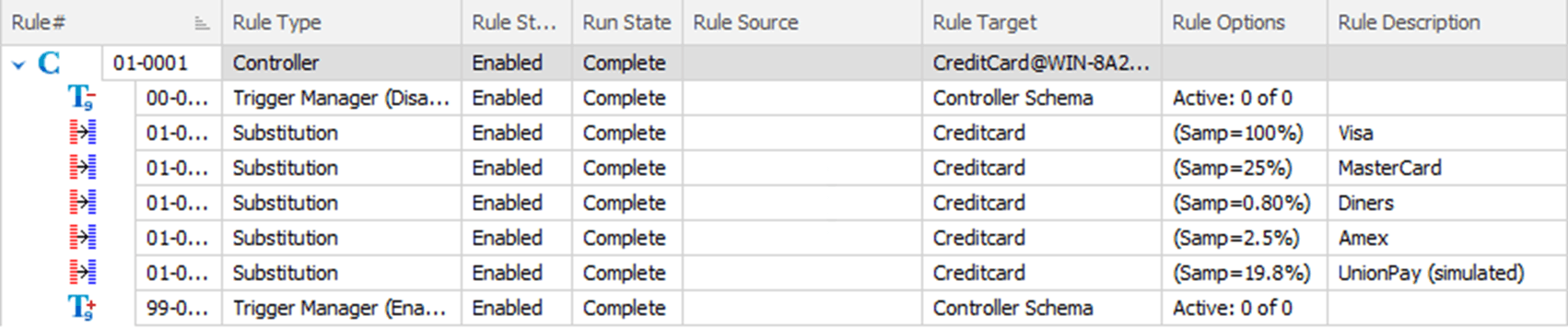
Figure 1
What we have here is a series of Substitution rules, one for each credit card type, all based on the same Rule Target, Creditcard. The real trick to making this work is in the way I’ve implemented the sampling sizes. Based on the data above, 50% of all the credit cards should be Visa. However, instead of doing 50%, the first rule step uses 100% sampling with the Visa settings.
This guarantees that, rather than risk missing out some small percentage of the data, every row from the initial data set will be replaced. If I were starting from production data, this would fulfill my first and top priority: compliance. All the data would be masked. The subsequent steps contain the rules for each of the different credit card types, in each case setting their sample size to the exact distribution I want to achieve (leaving the remaining 50%, roughly, as Visa).
This means that some of the data gets updated more than once and, because data masker (by default) uses threading and runs all the rules simultaneously, we could see the same row get changed from MasterCard to Amex to Diners. The result, though, is that we should see a distribution that is very close to the reality I’m attempting to simulate, especially on larger data sets.
Drilling into the data substitution rules
Let’s drill down on one of the rules to see exactly how I’ve set this up. Figure 2 shows the Column & Datasets tab of the Mastercard substitution rule.
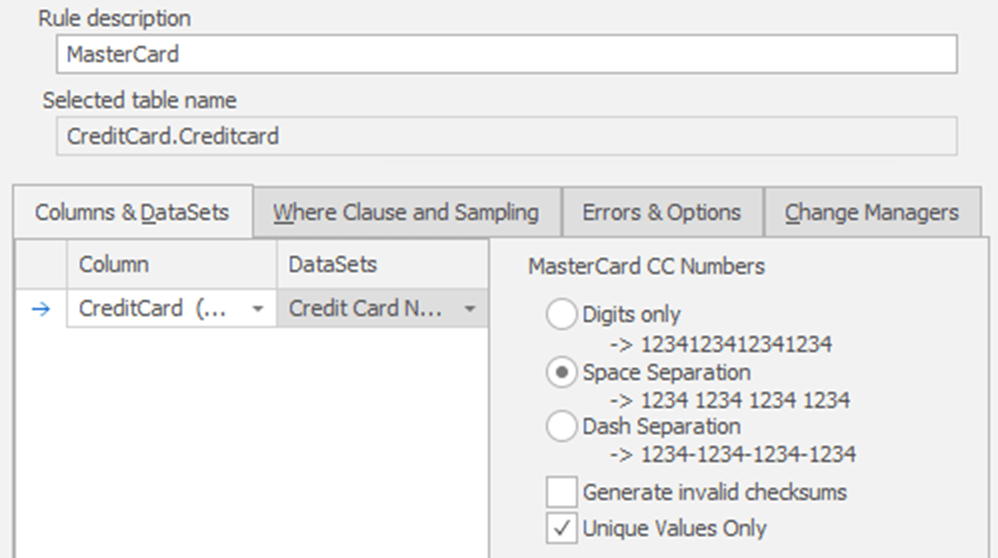
Figure 2
It’s within each of these individual rules that we can control the characteristics of the replacement data. You can see that I’ve defined my replacement MasterCard data to use Space Separation. I left Generate invalid checksums disabled, so that the credit card numbers generated would conform to the Luhn algorithm. I’ve also made sure that the data masker will generate only unique values. Obviously, you could change any of these settings depending on your requirements.
Figure 3 shows the Where Clause and Sampling tab for the same Mastercard substitution rule.
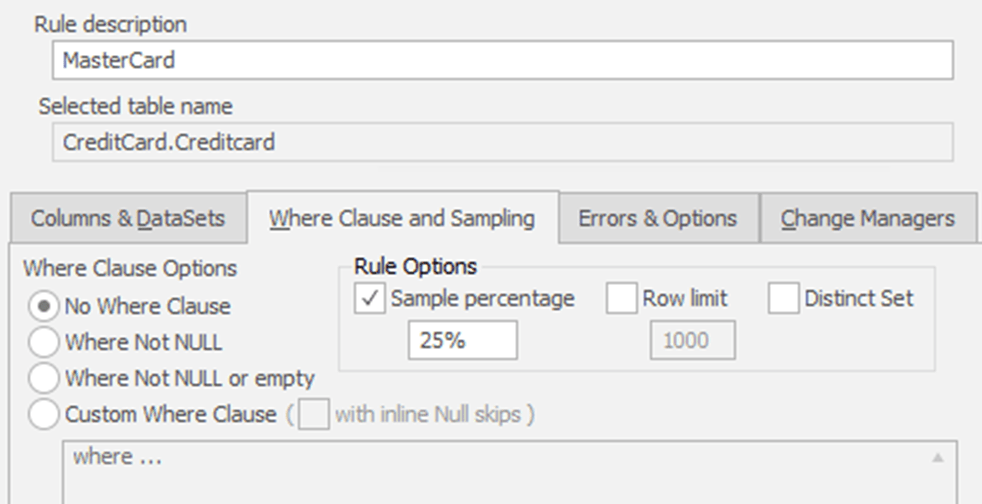
Figure 3
I’ve chosen not to use any kind of filtering on the data I’m updating because I have set up the table such that every row has data. This means that I don’t need to use the default setting of Where Not NULL or empty. I’ve also chosen a Sample percentage and set the value to the required value, 25% in this case.
That’s all there is to it. I create each rule, as shown, to arrive at a full set of credit card test data. If I rerun the query in Listing 1 against my new data set, I now see the following distribution, which will vary slightly every time you run the masking set:
| CreditTypePct | CreditCardType |
| 1.10 | 3 |
| 62.50 | 4 |
| 22.30 | 5 |
| 14.10 | 6 |
The Diners and Discover card type I used to simulate the UnionPay credit card has the same first digit, which is why this query returns only four card types instead of five. However, you can see that I do have a distribution of data that roughly mirrors the distribution I was aiming for.
Refining the data masking process by imposing a rule order
We could modify the data masking process to control more precisely how the data gets updated, while sacrificing some speed.
Instead of letting data masker run the each of the rules simultaneously, in a threaded fashion, as discussed earlier, I’m going to impose an order in which each rule should run, by adding Rule groupings, as indicated by the Rule Numbers in Figure 4.
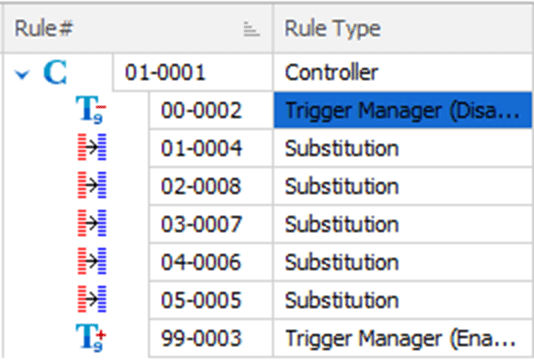
Figure 4
By modifying the rule number values such that the first two digits are in ascending order, from 1 to 5, I ensure that the previous rule will complete before the next one fires. The specific order I’ve chosen is to run the Visa rule first, to mask all the data (vital for compliance, as discussed earlier). After this first rule completes, I can be assured that all further substitutions will be performed against valid credit card values that contain information on a Visa credit card. Each of the subsequent rules run in order, in my case, from least to highest in terms of the amount of data being modified.
Finally, I’m adding a WHERE clause to my rules to ensure that data already modified doesn’t get modified again, as shown in Figure 5.
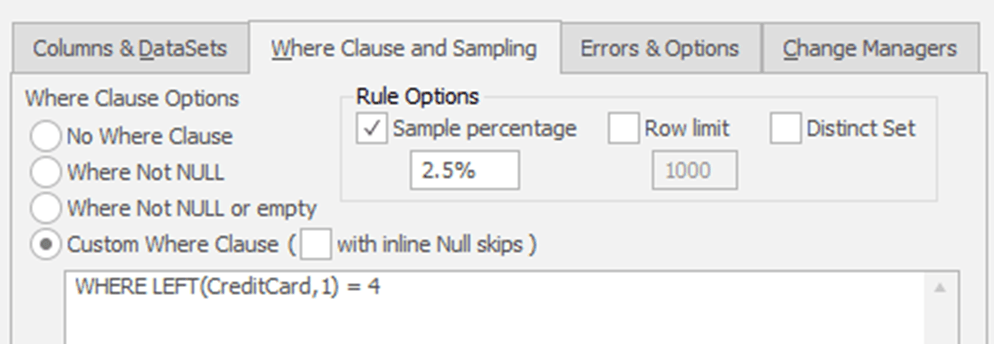
Figure 5
With this in place, the resulting distribution is much closer to our target distribution, and will be more consistent, if a little slower because of the filtering of the data as part of the data load process:
| CreditTypePct | CreditCardType |
| 3.10 | 3 |
| 58.30 | 4 |
| 19.40 | 5 |
| 19.20 | 6 |
Conclusion
Using data masking techniques like those described in this article, you’ll ensure that your test data is clean, and so meet the requirements of any data protection and privacy regulations. It will also look real, right down to small details such as the checksum values, and mirror a realistic distribution. All three of these are necessary steps in arriving at useful test data for your development and testing environments.
Now, I just need to go back and add an expiration date and CCV value to all my credit cards! Luckily there’s a Substitution Rule for credit card expiration dates and the CCV is just a three-digit random number, so this will be easy using Data Masker for SQL Server.
Data Masker for SQL Server can also be found as a part of the SQL Provision solution. Find out more about SQL Provision and grab your 14-day fully functional free trial.
Tools in this post
Data Masker
Shield sensitive information in development and test environments, without compromising data quality
SQL Provision
Provision virtualized clones of databases in seconds, with sensitive data shielded



